五道无人能解的简单数学题 [美国媒体]

5 Simple MathProblems No One Can Solve

五道无人能解的简单数学题

Easy to understand, supremelydifficult to prove.

易懂，却超级难证明



美国大众机械杂志网站
By AveryThompson
Oct 14, 2016

Mathematics canget pretty complicated. Fortunately, not all math problems need to beinscrutable. Here are five current problems in the field of mathematics thatanyone can understand, but nobody has been able to solve.

数学可以是非常复杂的。幸运的是，并非所有的数学题都那么的高深莫测。以下有五道当今数学领域的难题，大家都能看懂，然而却没人能够证明。

CollatzConjecture

考拉兹猜想



Pickany number. If that number is even, divide it by 2. If it's odd, multiply it by3 and add 1. Now repeat the process with your new number. If you keep going,you'll eventually end up at 1. Every time.

取任意一个数字，如果是偶数则除以2，如果是奇数就乘以3再加1。对所得到的新数字重复上述过程，最后你会发现，你总能最终得到数字1。每次都是。

Mathematicianshave tried millions of numbers and they've never found a single one that didn'tend up at 1 eventually. The thing is, they've never been able to prove thatthere isn't a special number out there that never leads to 1. It's possiblethat there's some really big number that goes to infinity instead, or maybe anumber that gets stuck in a loop and never reaches 1. But no one has ever beenable to prove that for certain.

数学家们尝试了数以百万计的数字，最后发现所有的数字重复这个过程，最后都是得到1。也就是，没人能证明不存在一个数字，这个数字在经过上述过程后最终得到1以外的数字。也许有存在非常大的数字最终的结果是除不尽，或者在这个过程中陷入无穷循环而没法最终得到1。至今这个结论都没人能证明。

MovingSofa Problem

移动沙发猜想



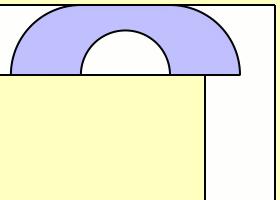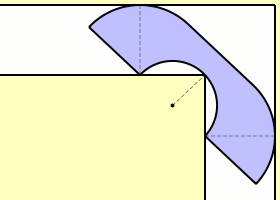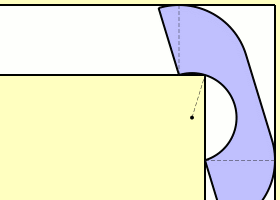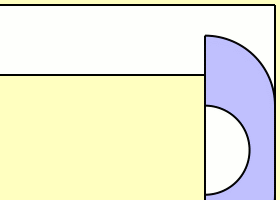
Soyou're moving into your new apartment, and you're trying to bring your sofa.The problem is, the hallway turns and you have to fit your sofa around acorner. If it's a small sofa, that might not be a problem, but a really bigsofa is sure to get stuck. If you're a mathematician, you askyourself: What's the largest sofa you could possibly fit around the corner? Itdoesn't have to be a rectangular sofa either, it can be any shape.

假设你要搬进新公寓，沙发需要搬进去。问题是，过道有转角。如果是个小沙发就不存在问题，但如果是个好大的沙发，那就会被堵住。如果你是个数学家，就会有这个问题：最大的可以绕过转角搬过去的沙发究竟是多大？转角不一定是直角，可以是任何形状的。

Thisis the essence of the movingsofa problem. Here are the specifics: thewhole problem is in two dimensions, the corner is a 90-degree angle, and thewidth of the corridor is 1. What is the largest two-dimensional area that canfit around the corner?

这就是移动沙发猜想的含义。让我们来给出条件：限定在2维，转角是90度，过道的宽度是1。刚刚好可以搬过转角的最大的二维面积是多大？

Thelargest area that can fit around a corner is called—I kid you not—the sofaconstant. Nobody knows for sure how big it is, but we have some pretty bigsofas that do work, so we know it has to be at least as big as them. We alsohave some sofas that don't work, so it has to be smaller than those. Alltogether, we know the sofa constant has to be between 2.2195 and 2.8284.

最大的可以搬过转角的二维面积被称作是-估计大家都没猜到-沙发常数。没人确切的知道是多大，不过我们有些相当大的沙发能搬过这个转角，所以我们知道至少这个数字不小于它们的面积：我们还知道有些沙发搬不过去，所以我们知道不能大于这些面积。这样以来，我们可以知道的是沙发常数是介于2.2195和2.8284之间。

PerfectCuboid Problem

完美长方体猜想（也叫PCP猜想）



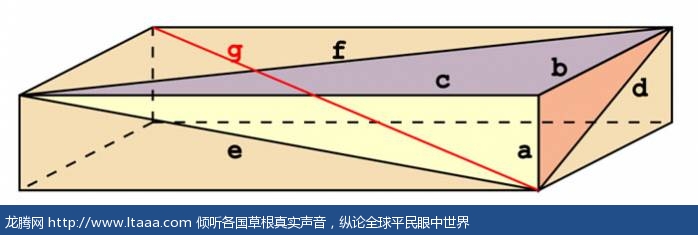
Rememberthe pythagorean theorem, A2 +B2 =C2? The three letters correspond tothe three sides of a right triangle. In a Pythagorean triangle, and all three sidesare whole numbers. Let's extend this idea to three dimensions. In threedimensions, there are four numbers. In the image above, they are A, B, C, andG. The first three are the dimensions of a box, and G is the diagonal runningfrom one of the top corners to the opposite bottom corner.

还记得勾股定理吗，A2 +B2 =C2 ？三个字母分别代表直角三角形的三条边。在一个勾股三角形中，可以三个边都是整数。让我们将这个带到三维空间。在三维空间，有四个数字。在附图中，分别是A、B、C和G。前三个是盒子的三维尺寸，G是从上顶角到斜对底顶角的长度。

Justas there are some triangles where all three sides are whole numbers, there arealso some boxes where the three sides and the spatial diagonal (A, B, C, and G)are whole numbers. But there are also three more diagonals on the threesurfaces (D, E, and F) and that raises an interesting question: can there be abox where all six of these lengths are integers?

就像三角形那样，存在着三边都是整数的情形，也存在着A、B、C和G都是整数的组合。如果再看看盒子上的另外三条对角线D、E和F，是否存在一个这样的盒子，使得上述6个长度都是整数呢？

The goal isto find a box where A2 +B2 +C2 =G2, and where all six numbers areintegers. This is called a perfect cuboid. Mathematicians have tried manydifferent possibilities and have yet to find a single one that works. But theyalso haven't been able to prove that such a box doesn't exist, so the hunt ison for a perfect cuboid.

这个猜想就是要找到一个这样的盒子，它满足A2 +B2 +C2 =G2，以及6个数字都是整数，这种长方体就是完美长方体。数学家们费尽脑汁都没找到一个符合的长方体，不过也没人能证明这样的长方体不存在，所以这还是一个等待解决的猜想。

Inscribed Square Problem

内接正方形猜想



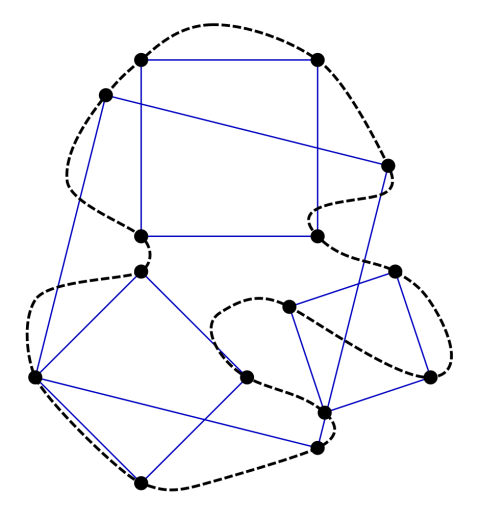
Drawa closed loop. The loop doesn't have to be a circle, it can be any shape youwant, but the beginning and the end have to meet and the loop can't crossitself. It should be possible to draw a square inside the loop so that all fourcorners of the square are touching the loop. According to the inscribedsquare hypothesis, everyclosed loop (specifically every plane simple closed curve) should have aninscribed square, a square where all four corners lie somewhere on the loop.

画一条封闭的曲线。这条曲线不一定是一个圆，可以是任意曲线，只要起始点和终结点重合、曲线自身不相交，那么总是能在曲线上取4个点画出一个内接正方形。根据内接正方形猜想，每个封闭的曲线（也就是每个平面简单闭曲线）都存在一个内接正方形，该正方形的四个顶点均在该曲线上。

Thishas already been solved for a number of other shapes, such as triangles andrectangles. But squares are tricky, and so far a formal proof has eludedmathematicians.

其他的几个形状都被证明了，包括三角形和长方形。然而正方形比较诡异，目前数学家们都被难倒了。

Happy Ending Problem

幸福结局猜想



The happyending problem isso named because it led to the marriage of two mathematicians who worked on it,George Szekeres and Esther Klein. Essentially, the problem works like this:

这个猜想的名字源自两位研究这个难题的数学家GeorgeSzekeres和EstherKlein，他们最终因为都研究这个难题而喜结姻缘。这个难题如下所述：

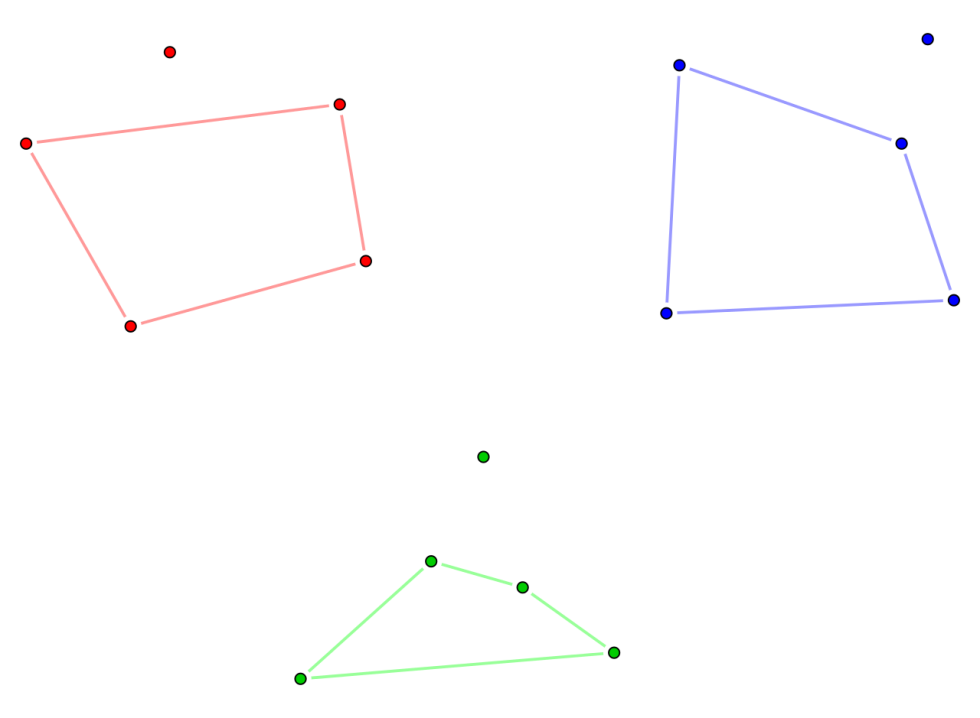
Makefive dots at random places on a piece of paper. Assuming the dots aren'tdeliberately arranged—say, in a line—you should always be able to connect fourof them to create a convex quadrilateral, which is a shape with four sideswhere all of the corners are less than 180 degrees. The gist of this theorem isthat you'll always be able to create a convex quadrilateral with five randomdots, regardless of where those dots are positioned.

在纸面上随机点5个点，假设这些点不是在一条直线上，你总能把其中的四个点连成一个凸四边形，也就是所有的四个内角都小于180度。这个定律就是，你总能画出一个凸四边形，无论这些点如何分布。

Sothat's how it works for four sides. But for a pengaton, a five-sided shape, itturns out you need nine dots. For a hexagon, it's 17 dots. But beyond that, wedon't know. It's a mystery how many dots is required to create a heptagon orany larger shapes. More importantly, there should be a formula to tell us howmany dots are required for any shape. Mathematicians suspect the equation isM=1+2N-2, where M is the number of dotsand N is the number of sides in the shape. But as yet, they've only been ableto prove that the answer is at least as big as the answer you get that way.

四边形就是这样。然而对于五边形，却需要9个点；对于六边形，需要17个点。超出六边形的其他多边形，我们就不知道了。对于七边形及更多角的多边形，我们不知道需要多少点。更重要的是，应该存在一个公式，我们可以计算出对于任意多边形，我们需要多少个点。数学家怀疑这个公式是M=1+2N-2｛1+2的（N-2）次方｝，式中M代表需要的点数，而N代表多边形的边数。不过迄今为止，数学家们只能证明需要的点数不小于是这样计算出来的数字。